5. Problém obchodního cestujícího
Zadání:
Je dáno m měst. Některá města jsou
propojena silnicemi, délka silnic je známa. Úkolem obchodního cestujícího
je navštívit všechna města (právě jednou, aspoň jednou, uvažujte případ,
který se Vám víc líbí) a vrátit se do výchozího města. Nalezněte takovou
tůru (permutaci měst), aby délka uražené cesty byla co nejmenší.
Navrhněte a implementujte algoritmus řešící
problém obchodního cestujícího. Funkčnost algoritmu ověřte na sadě dodaných
testovacích příkladů (ve všech třech variantách - viz
níže).
Poznámky: Předpokládáme, že budete implementovat
nějaký iterativní algoritmus (pokud možno nějakou z pokročilých iterativních
metod). Určitě vyzkoušejte a popište vliv počátečního stavu na kvalitu
nalezeného řešení.
Testovací příklady jsou ohodnocené
neorientované grafy zadané uzlovou maticí. Ohodnocení jedné hrany (koincidence
uzel-uzel) je reprezentováno jedním znakem v matici (vlastně dvěma, neboť
se jedná o neorientované grafy). Ohodnocení hrany je určeno pořadím znaků
'1'-'9', 'A'-'Z', '0' znamená, že hrana mezi uzly neexistuje (viz popis
níže). Hodnota hrany se spočítá
if (matice[a][b]=='0')
tak tam žádná hrana není /* viz popis níže */
if ((matice[a][b]>='1') && (matice[a][b]<='9'))
hodnota=matice[a][b]-'0';
else if ((matice[a][b]>='A') && (matice[a][b]<='Z'))
hodnota=matice[a][b]-'A'+10;
Neexistující hrany
(tzn. hrany s hodnotu '0') zpracujte třemi způsoby:
- Hrany existují a mají hodnotu 10.
- Hrany existují a mají hodnotu 10000.
- Hrany neexistují.
Příklady se jmenují a.txt, b.txt,
?.., k.txt. Protože se jedná
o docela velké soubory (až 4MB), jsou zabaleny v arj souboru tspbench.arj .
Pro odladění Vašich programů máte též k dispozici generátor grafů
- původně součást diplomové práce z University of Alberta. Program hcp
generuje neohodnocené grafy a hledá v nich Hamiltonovy kružnice různými
algoritmy. Program hcp2tsp dává hranám náhodné ohodnocení a převádí
grafy do formátu popsaného nahoře. Maximální velikost grafu je 1600 uzlů,
maximální stupeň uzlu je 50. Zdrojové texty obou programů:
hcp.tgz
Původní manuál
Program byl původně určen pro SunOS 4, nyní byl testován na
- SunOS 4.1.4 (gcc 2.7.2)
- Solaris 7 (SunOS 5.7) (gcc 2.95)
- FreeBSD 4.0 (gcc 2.95)
- DOS/DPMI (gcc 2.95)
Provoz na Linuxu nebyl zkoušen, nepředpokládáme obtíže. DOS verze má omezenou
funkčnost, neoť kód je poněkud fortranského střihu a alokuje na zásobníku
velká pole. Ověření existence Hamiltonovy kružnice se zpravidla nepodaří.
Oba programy jsou nainstalovány na CSLABu (Y:\VLSI\TSP), SunOS
4 (/usr.sw/bin) a Solaris 2 (/opt/bin).
Zpráva by měla kromě obvyklých náležitostí obsahovat
též tabulku udávající počet navštívených stavů stavového prostoru a tabulku
zachycující pořadí jednotlivých testovacích příkladů v závislosti na ceně
Vámi nalezené túry.
Řešení:
Rozhodl jsem se řešit zadání s navštívením každého města jen jednou - hledám tedy Hamiltonovu kružnici.
Začal jsem rekurzivním backtrackingem (prohledávání do hloubky).
Tento algoritmus pracuje tak, že k otevřenému uzlu hledá všechny jeho sousedy kteří ještě nejsou v posloupnosti
a zavolá sám sebe s nově otevřeným uzlem. Zapsáno pseudokódem:
void BackTracking(int openNode)
{
if (IsHamilton()) // nalezen
{
Merge(openNode, startNode) // spoj posledni s prvnim
if (IsBestHamilton()) // nalezene je nejlepsi
SaveBestHamilton() // uloz nejlepsi
Merge(openNode, -1) // zrus posledni spoj
return
}
for (i=0; i<countNodes; i++)
{
if (IsPath(openNode,i) && !InPath(i)) // je cesta mezi otevrenym a testovanym
{
Merge(openNode, i) // spoj je
BackTracking(i) // zavolej sam sebe
Merge(openNode, -1) // rozpoj je
}
}
}
Tato bruteforce metoda byla podle očekávání nepoužitelně pomalá a nehodí se ani k nalezení první kružnice.
Z pokročilích iterativních metod - simulované ochlazování, genetický algoritmus, tabusearch -
jsem se z časových důvodů rozhodl pro simulované ochlazování, která mi přišla
silná a jednoduchá na iplementaci.
Tuto metodu lze popsat zjednodušeně takto:
Simulated Cooling()
{
state=InititState() // nalezeni libovolneho vychoziho stavu
temp=temp0 // nastaveni pocatecni teploty
repeat
repeat
state=TryState(state, temp) // zkouska jineho reseni
until Equilibrium(state, temp) // rovnovaha (zavisla na poctu iteraci, teplote apod)
temp=Cool(temp); // ochlazeni teploty
until !Frozen(temp) // teplota klesla pod urcitou mez
return state
}
TryState(state,temp)
{
new=NewNeighbour(state); // nalezeni noveho reseni
delta=Cena(state)-Cena(new)
if (delta>0) // nove je lepsi => prijmem
return new;
else // nove je horsi => mozna prijmem
if (random<e^(delta/temp)
return new;
else
return state;
}
Funkce InitState nalezne nějaké počáteční řešení (v našem případě L.Posovo heurestikou - viz. níže).
TryState se stará o změnu aktuálního řešení a její akceptování/zamítnutí
(pokud je nalezené řešení lepší akceptuje se vždy, v opačném případě o akceptování rozhodne pravděpodobnost
závislá na teplotě a velikosti zhoršení ceny).
Equilibrium stav rovnováhy, v našem případě závislé na počtu iterací.
Cool snižuje simulovanou teplotu
(v našem případě podle vzorce temp_new=temp*0,98, kde 0,98 bylo nastaveno po několika experimentech).
Frozen test dosažené teploty pro ukončení algoritmu, opět experimentálně nastaveno na 0,07.
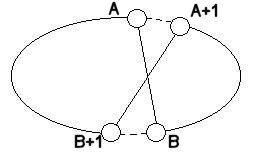
NewNeighbour je řešen dvojzáměnou -
pokud vede cesta z a do b a zároveň z a+1 do b+1
spojí se a s b a a+1 sb+1.
Posova herestika funguje na principu postupného prodlužování
a modifikování již nalezené cesty. Vysvětlující pseudokód můžeme zaspat např. takto:
PosovHeuristics()
{
InitFirstNode() // vyber startovniho mesta
while(iteration<maxIter) // omezeni doby hledani cesty
{
while (Extension()) {} // dokud jde prodluzovat prodluzuj
if (IsHamilton())
return true // hamilton nalezen
else
{
Modify() // zmen cestu
}
}
return false // hamilton nenalezen
}
Kde funkce InitFirstNode vybere startovní uzel. Může vybrat například náhodně nebo
uzel s největším/nejmenším stupněm. Já jsem použil první uzel v matici.
Extension připojuje k poslednímu uzlu v doposavaď nalezené cestě další zatím
nenavštívený uzel, dokud je to možné.
Funkce Modify se použije v momentě kdy již nelze stávající cestu dál prodlužovat.
Projde postupně všechny uzly nalezené cesty a pokud nalezne uzel x ze kterého existuje spoj do
posledního uzlu v cestě, spojí x s posledním uzlem a provede otočení směru cesty
mezi posledním uzlem a uzlem x+1, jak je znázorněno na obrázku.
Použité datové struktury jsou všechny alokovány staticky.
V poli short matrix[][] je uložena matice sousednosti neorientovaného grafu
(symetrická podle hlavní diagonály vyplněné nulami). Pole short track[] reprezentuje
aktuální posloupnost nalezené Hamiltonovy kružnice, kde index je pořadí uzlu v kružnici a hodnota
číclo uzlu v matici sousednosti.
Naměřené hodnoty:
Proměnné použité při měření:
počáteční teplota=50
freeze: při teplotě<0,07 nebo pokud již 5 ochlazení nedošlo ke zlepšení
cool: teplota=teplota*0,95
maximální počet modifikací v Posonově heurestice=počet_uzlů*500
Do tabulky jsem zanesl nejlepší hodnotu ze tří provedených měření (lišících se jen ve startovním bodě).
| soubor |
počet měst |
délka hamlitonovi kružnice |
| 0 - hrana neexistuje |
0 - hrana délka 10 |
0 - hrana délka 10000 |
| suboptimální |
první |
konečné |
první |
konečné |
první |
konečné |
| testik.txt |
81 |
- |
581 |
135 |
567 |
145 |
50513 |
140 |
| a.txt |
2187 |
3729 |
20039 |
19722 |
16779 |
14641 |
7259529 |
19766 |
| b.txt |
625 |
3905 |
3940 |
2224 |
3185 |
1636 |
1201984 |
2222 |
| c.txt |
2187 |
3729 |
17649 |
17630 |
16761 |
15140 |
7299471 |
145728 |
| d.txt |
200 |
384 |
1001 |
633 |
606 |
491 |
20591 |
662 |
| e.txt |
256 |
423 |
2685 |
670 |
273 |
337 |
20253 |
675 |
| f.txt |
2187 |
3729 |
19340 |
19277 |
16756 |
15092 |
7269499 |
66357 |
| g.txt |
1296 |
906 |
nenalezl |
nenalezl |
6267 |
5793 |
2174097 |
375858 |
| h.txt |
236 |
neexistuje |
nenalezl |
nenalezl |
271 |
300 |
40231 |
10693 |
| i.txt |
2187 |
3729 |
nenalezl |
nenalezl |
16762 |
15298 |
7299471 |
1613180 |
| j.txt |
2048 |
3070 |
21685 |
21482 |
20502 |
19535 |
10170343 |
22721 |
| k.txt |
1296 |
906 |
12701 |
12542 |
6269 |
5635 |
2164101 |
66845 |
Závěr:
Při malém počtu uzlů a doplnění neexistujícich hran se ve třech případech stalo, že zoptimalizovaná délka
byla o něco delší než první nalezená. Mé nastavení teplot se tedy pro takovéto případy příliš nehodí.
Další problém (ve dvou případech) je nenalezení výchozí cesty, zde by bylo řešení prodloužit délku
výpočtu Posovo heurestiky.
Výhoda nahrazení cesty nulové délky velkou hodnotou je v okamžitém nalezení počáteční hamiltonovi kružnice,
v následné optimalizaci by pak tyto dlouhé hrany měly být vyloučeny (což se v mém případě opět příliš nepovedlo).
Naopak zdržení nastává při optimalizaci, protože z dříve řídkých grafu se staly grafy úplné,
dojde tedy k většímu počtu možných záměn.
Bohužel se mi nepodařilo řešení odladit k úplné spokojenosti. Změna počáteční teploty příliš velký vliv
na výsledné řešení neměla. Také volba startovního města pro Posonovu heurestiku přináší rozdíly jen v řádu
jednotek procent. Zlepšením by zřejmě bylo vylepšení algoritmu o cyklického žíhání.
Ve většině případů jsem se tedy k doposud nejlepším známým kružnicím příliš nepřiblížil
(kromě zadání b.txt, kde je mé řešení lepší, než řešení uvedené na stránkách tohoto předmětu).
Přílohy:
zdrojový kód tsp.cpp
zakompresovaná data použitá v analýze data.rar